We use different measurement units to determine length (in, m, or km), mass (kg, mg, or g), or temperature (Celsius or Fahrenheit) and Math enables us to convert between these measurement units. In the same way, a circle’s angle can be measured in two ways: with degrees and with radians and using formulas, we can convert between the two.
What is Radian Measure?
Recall that a degree of an angle (°) measures the rotation between each arm. A full rotation or revolution is 360° and a half-circle rotation is 180°. To understand radian measure or radian (rad), we must first discuss central angle –an angle whose vertex is at the center of a circle. A central angle’s radian is measured by its corresponding arc whose length is equal to the radius. In other words, radian is the angle measure of the resulting arc when the radius is curved around the circle’s circumference. See illustration below.
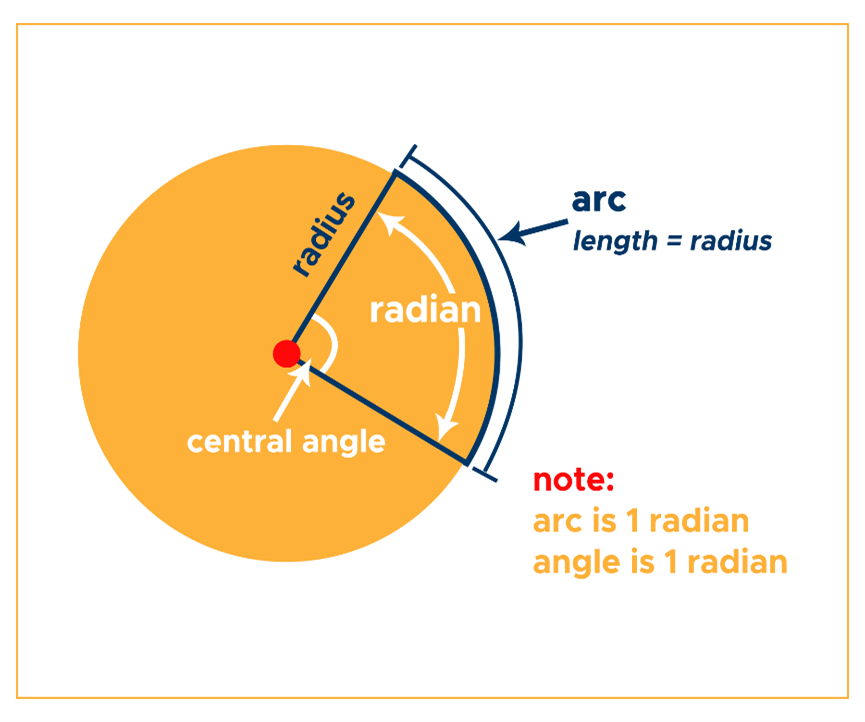
A central angle of 360° has a radian of 2π as expressed in the equation:
2π radians = 360°
Dividing this by 2 gives us 1π radian = 180° which we’ll use to convert between the two measurement units.
How to Convert Between Degrees and Radians:
Use the formulas below to convert between degrees and radians.

To convert from degrees to radians,
multiply the number of degree by π / 180°.
To convert from radians to degrees,
multiply the radians by 180° / π .
Examples:
- What is the radian measure of 150°?
Solution:
Multiply 150° by π / 180°.
150° x (π / 180°) = (150π / 180°) = (5π / 6) radians or ≈ 0.83π radians.
Note: The degree units in 150° and 180° were cancelled out during multiplication. - What is the radian measure of 36°?
Solution:
Multiply 36° by π / 180°.
36° x (π / 180°) = (36π / 180°) = (π / 5) radians or ≈ 0.2π radians. - What is the degree measure of an arc whose measure is 3π / 8 radians?
Solution:
Multiply 3π / 8 by 180° / π.
(3π/ 8) x (180° /π) = 540° / 8 = 67.5° - What is the degree measure of an arc whose measure is 1.8π radians?
Solution:
Multiply 1.8π by 180° / π.
1.8πx (180° /π) = 324° - What is the degree measure of an angle whose measure is 12 radians?
Solution:
Multiple 12 by 180° / π.
12 x (180° / π) = 2160° / π ≈ 687.9°
Thank you for reading. We hope it’s effective! Always feel free to revisit this page if you ever have any questions about converting degrees to radians.
Check out some of our other blog posts or invest in your future with one of our self-study courses!


