A square is a shape with four equal sides (equilateral) and four equal angles (equiangular). It’s the only equilateral and equiangular quadrilateral. Here’s a quick guide to computing the area of a square.
How to Compute the Area of a Square
The area of a shape refers to the total amount of space enclosed in it. To find the area of a square, multiply Base by Height, as expressed in the formula A=BH; however, since a square has equal sides, we can write the formula as:
A = s • s
where: s = length of one side of the square
Example. Find the area when given 12cm length.
A = s • s
Let s be 12cm
A = 12cm • 12cm
A = 144 cm2
The illustration below that shows the formulas for the area and perimeter of a square.
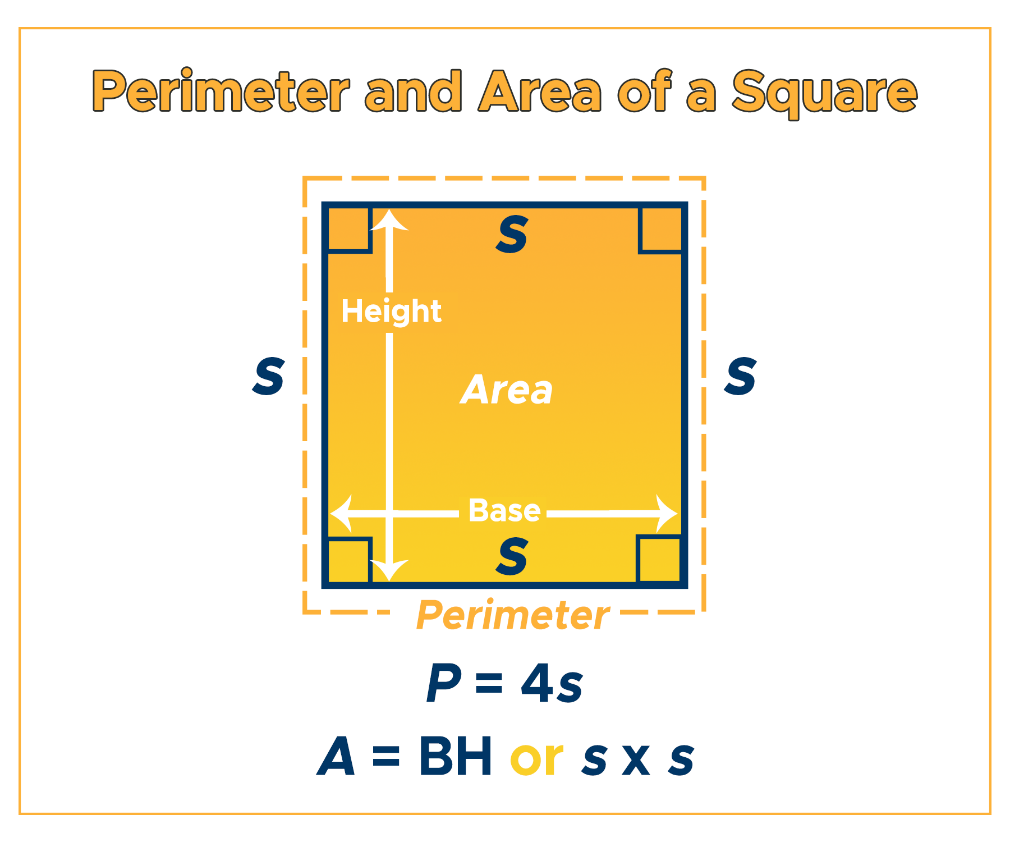
Want to learn more about finding the perimeter of a square?
Related Reading: Perimeter of a Square – Formula & Examples
Example #1: Compute the area of a square with a length of 11 inches.

Solution for Example #1:
Substitute 11 inches for s in the area formula, A = s • s.
A = 11 in • 11 in
A = 121 in2
Therefore, the area is 121 in2.
Example #2: Find the area when given a length of 5.5 meters.
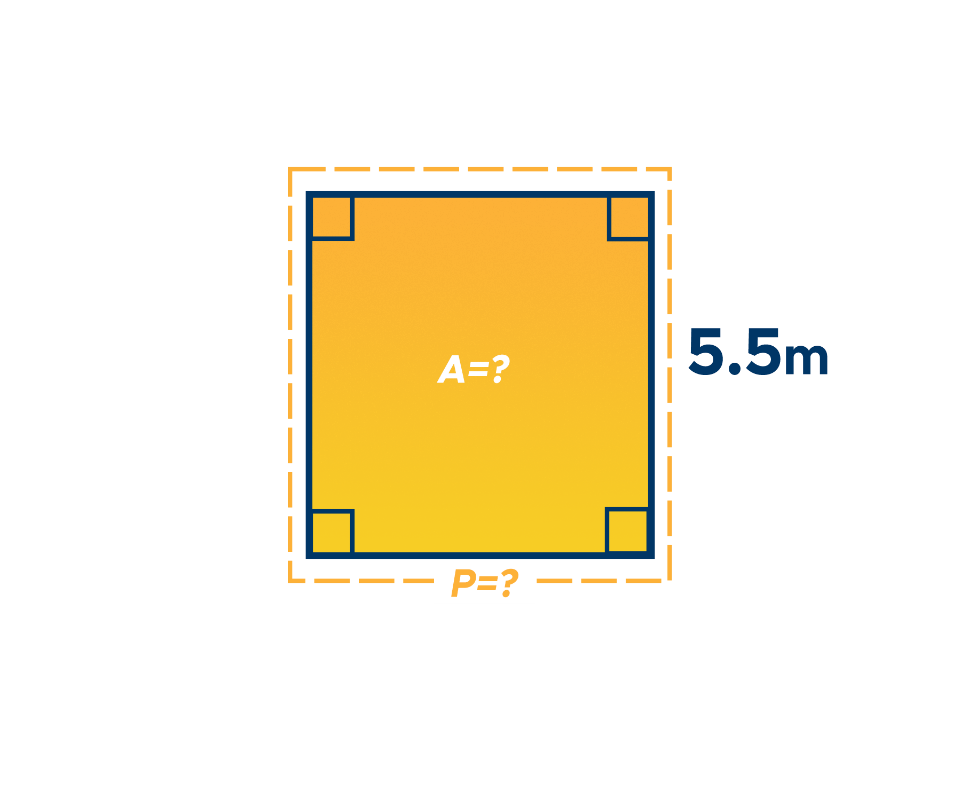
Solution for Example #2:
Substitute 5.5 meters for s in the perimeter formula, A = s • s.
A = 5.5 m • 5.5 m
A = 30.25 m2
Therefore, the area is 30.25 m2.
Example #3: Find the length of a side of a square when given an area of 64 cm2.
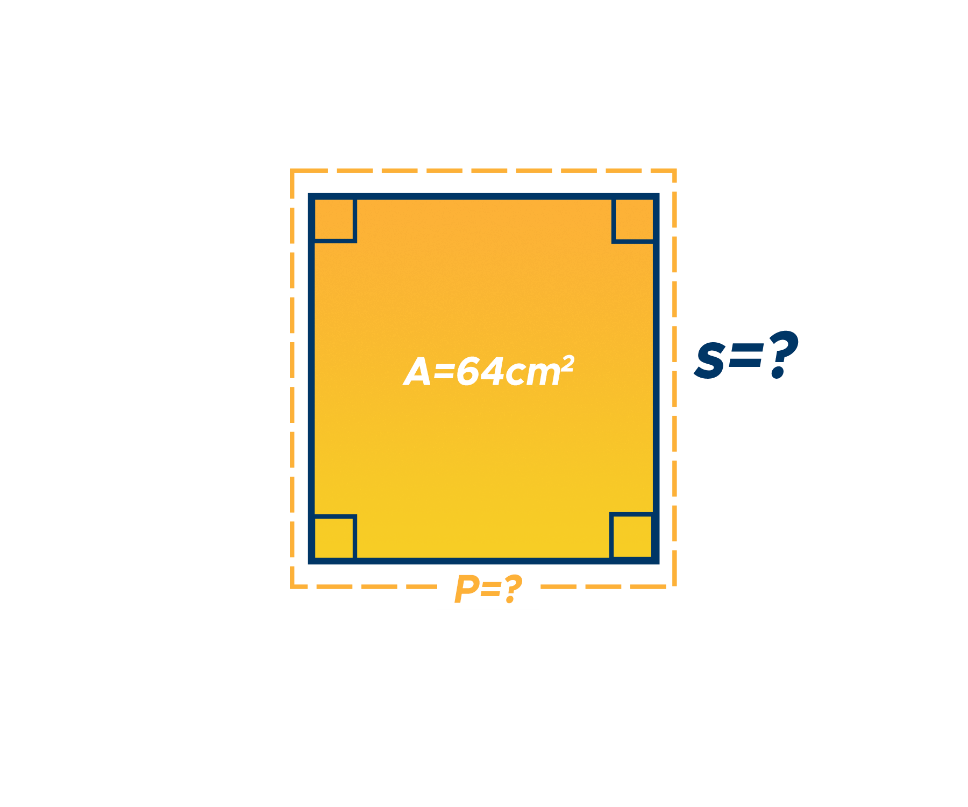
Solution for Example #3:
Compute the length of the sides by taking the square root of A.
Use the formula: s = √A
Substitute 64 cm2 for A.
s = √(64 cm2)
s = 8 cm
Therefore, the length of the sides of the square are 8 cm.
Thank you for reading. We hope it’s effective! Always feel free to revisit this page if you ever have any questions about the area of a square.
Check out some of our other blog posts or invest in your future with one of our self-study courses!


